Forget FOIL, multiply with rectangles!
We’re going to take a quick trip down elementary-high-school-algebra lane, and explore an alternative to the commonly taught method of multiplying two binomials known as FOIL. This is the kind of expression I’m talking about:
(x – 2)(x + 6)
This expression can be easily simplified using FOIL, provided you remember what the acronym stands for in the first place. But the problem is that FOIL is only useful for problems that look exactly like the one above. So what happens if your sadistic math teacher throws you a curve ball like this:
(x – 2 + y)(x + 6)
If all you were ever taught was to FOIL, you might be left scratching your head. Of course anyone who’s got a good grasp on math would know that you just need to multiply each term in the left polynomial by each term in the right polynomial. However if all you ever learned was the FOIL method and you’re not all that great at math, this might not be obvious to you. Thankfully there’s another way that is easier to visualize, and will hopefully make your life much easier. From this point on I want you to forget anything you ever heard about FOIL, it’s not useful anymore.
Thinking about these expressions geometrically should help them make a bit more sense, this is where the rectangles come in. We know that when you multiply the lengths of two perpendicular sides (width and height) of a rectangle you are left with the area of that rectangle. This is precisely what’s going on in the expressions above, we can imagine that each expression in parenthesis describes the lengths of two sides of a rectangle. It looks like this:
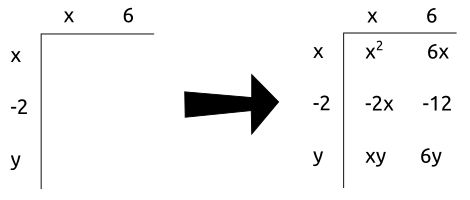
We will set up our rectangular multiplication like the left side of the above image. Proceed to multiply each row + column intersection and you will end up with a filled table like the one you see on the right of the image. Once you’ve multiplied all the terms, you can combine like terms and see the completed simplification:
x2 + xy + 4x + 6y – 12
That’s all there is to it! I have to thank my Math 118 professor Reid Huntsinger for explaining this. It would be nice if high school math teachers would drop FOIL for a method that makes more sense, and gives you a better understanding of what’s really going on.

